Gauge Fields
Gauge fields are found in the modern description of gravity and the most fundamental interactions known in our Universe, but they also appear when describing why a cat always lands on its feet. Gauge fields are both physical entities and useful resources that help us sharpen our understanding of the world.
We explore the ability of certain gauge fields to deeply alter the properties of quantum matter and even its mere identity. These dramatic effects become palpable when said fields back-act on matter. Things get even more exotic when robust structures known as topological solitons are present in the systems under study.
Synthetic Gauge Fields
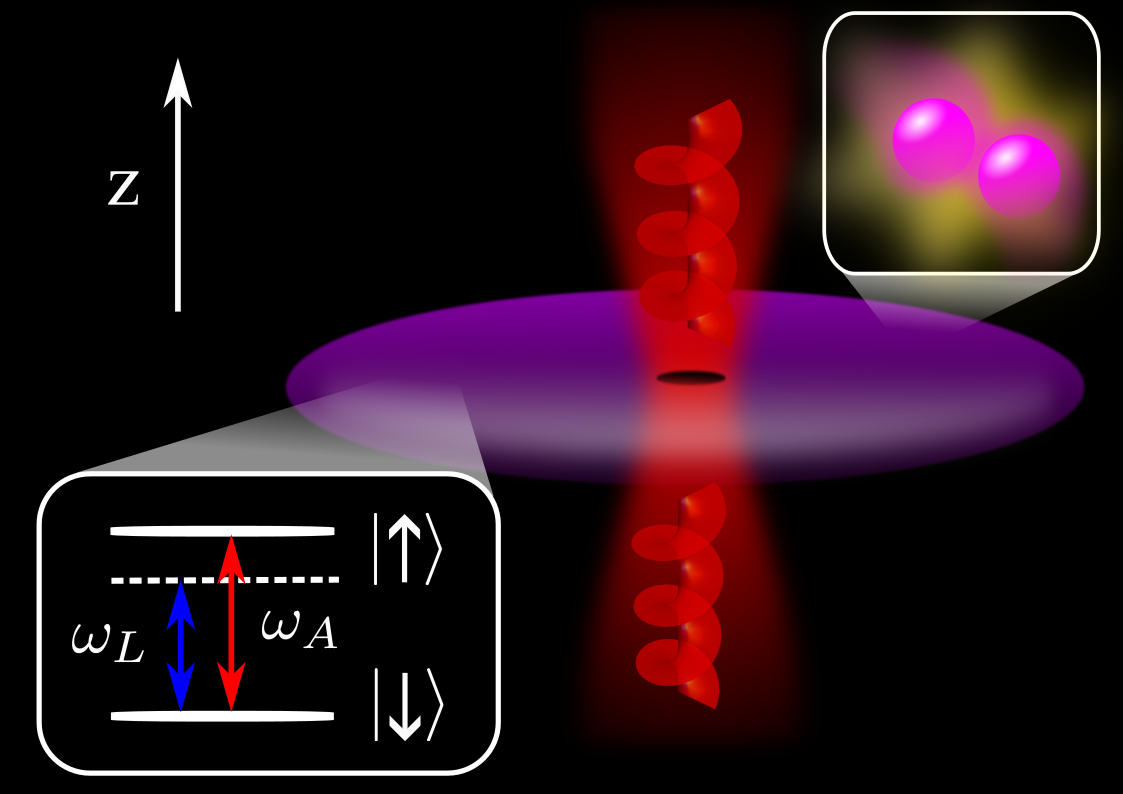
Ultracold atoms acting as quantum simulators constitute an invaluable platform for the study of quantum many-body physics and beyond. This is mainly due to the exquisite control achieved in the last decades and the enormous versatility of the setup. An intrinsic limitation, however, is the lack of natural interaction of atoms with gauge fields due to their intrinsic charge neutrality. In short, there is no Lorentz force, and thus no minimal coupling. This is a serious obstruction for the emulation of systems like those of condensed matter where electrons do couple to gauge fields, and with special relevance to the growing interest in topological quantum matter, fundamentally tied to the presence of gauge fields. This is why soon after the creation of the first BECs several works on artificial or synthetic gauge fields appeared. These are mathematical objects that have similar properties to conventional gauge fields and minimally couple to matter regardless of whether it is charged or not. Hence, they can make ultracold atoms (or any other system) respond to the presence of electromagnetic fields.
Topological Gauge Fields
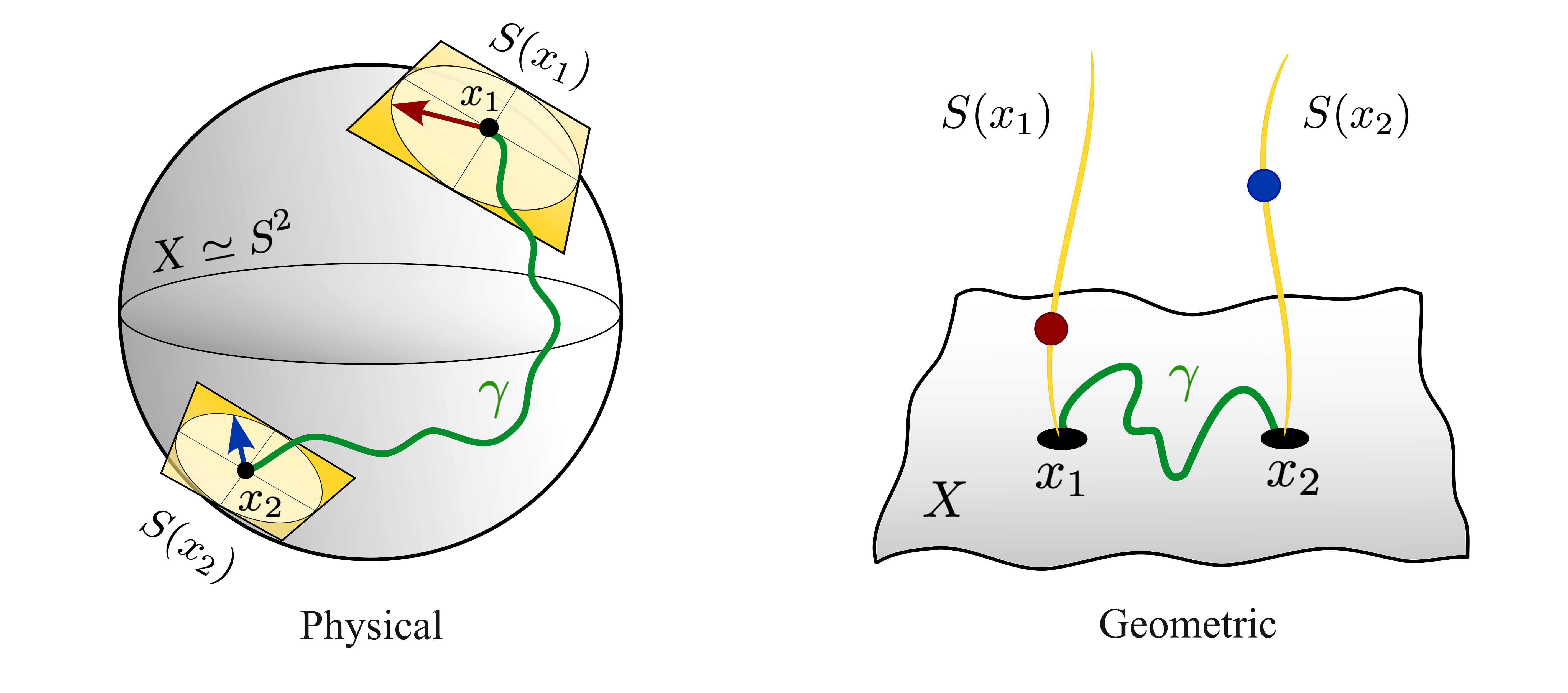
An incredibly subtle but important concept in modern Physics is that of topological terms. A theory purely containing these terms is known as a topological field theory. When the fields in such theories are or can be recast in terms of gauge fields, we talk about topological gauge theories. We use this terminology more loosely to describe those theories, in general coupled to matter, in which topological gauge terms are present. In a nutshell, these describe systems in which the gauge field presents topological features. Roughly speaking, these features come in the form of twists, singularities, discontinuities, branch-cuts, or other ill-defined countable mathematical objects, that are found in the target space of a gauge potential or its field strength. These defects seed topological invariants that label robust sectors or regimes in which the systems can be found. There is a deep connection between quantum anomalies, topological terms, fractional fermion numbers, index theorems, and geometric phases that is often difficult to make explicit.
