Themes
Quantum Error Correction
The accumulation of errors in quantum computers obstructs the execution of powerful algorithms. Hence, current quantum computers require Quantum Error Correction (QEC) in order to be functional and reliable even in the presence of such errors, something known as Fault-Tolerant Quantum Computation (FTQC). The implementation of quantum error-correcting codes was not possible with Noisy Intermediate-Scale Quantum (NISQ) era devices but, as we move past this initial stage in quantum technologies, it becomes a necessary step for progress and a pressing issue for current architectures.
Conventional strategies for protecting and correcting against qubit errors, such as Surface codes, suffer from large overheads in the number of physical qubits that are used to encode logical information. In other words, practical implementation of quantum error-correcting codes requires a better ratio between the number of logical and physical qubits, something known as a high encoding rate.

Gauge Fields
Gauge fields are found in the modern description of gravity and the most fundamental interactions known in our Universe, but they also appear when describing why a cat always lands on its feet. Gauge fields are both physical entities and useful resources that help us sharpen our understanding of the world.
We explore the ability of certain gauge fields to deeply alter the properties of quantum matter and even its mere identity. These dramatic effects become palpable when said fields back-act on matter. Things get even more exotic when robust structures known as topological solitons are present in the systems under study.
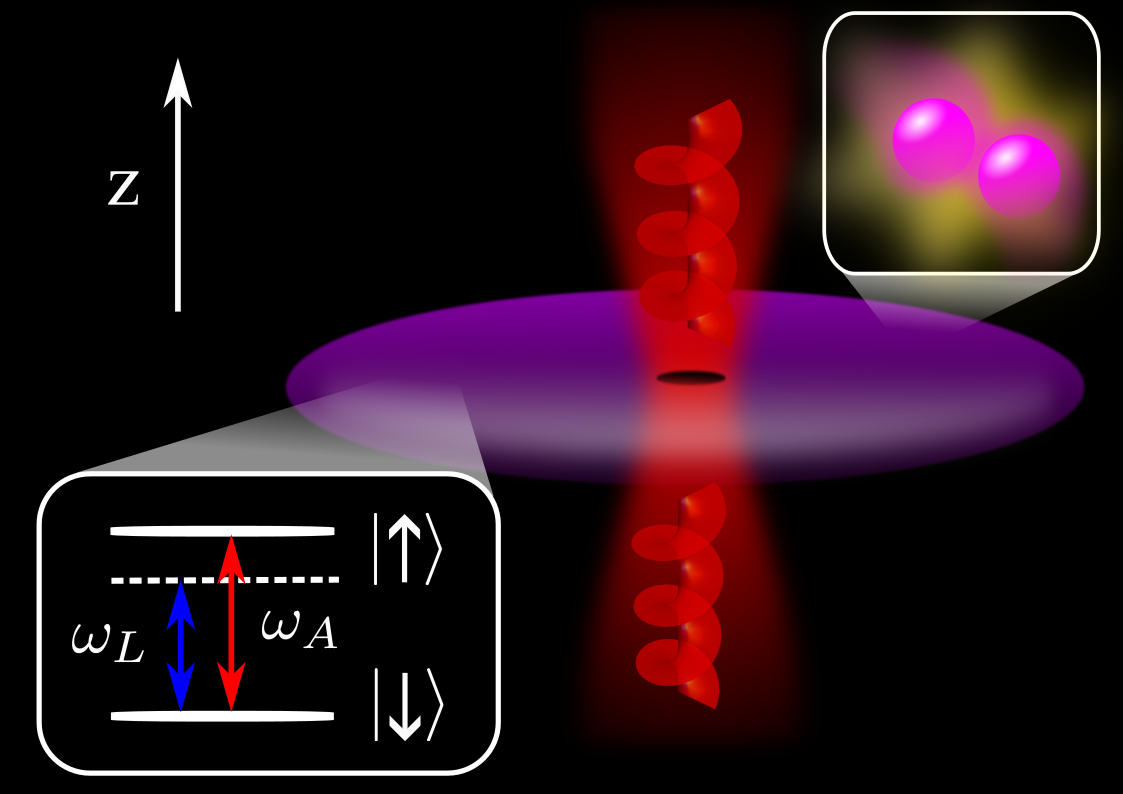
Synthetic Gauge Fields
Ultracold atoms acting as quantum simulators constitute an invaluable platform for the study of quantum many-body physics and beyond. This is mainly due to the exquisite control achieved in the last decades and the enormous versatility of the setup. A major limitation, however, is the lack of natural interaction of atoms with gauge fields due to their intrinsic charge neutrality. In short, there is no Lorentz force, and thus no minimal coupling. This is a serious obstruction for the emulation of systems like those of condensed matter where electrons do couple to gauge fields, and with special relevance to the growing interest in topological quantum matter, fundamentally tied to the presence of gauge fields. This is why, soon after the creation of the first Bose-Einstein condensates, several works on artificial or synthetic gauge fields appeared. These are mathematical objects that have similar properties to conventional gauge fields and minimally couple to matter regardless of whether it is charged or not. Hence, they can make ultracold atoms (or any other system) respond to the presence of (pseudo) electromagnetic fields.
Topological Gauge Fields
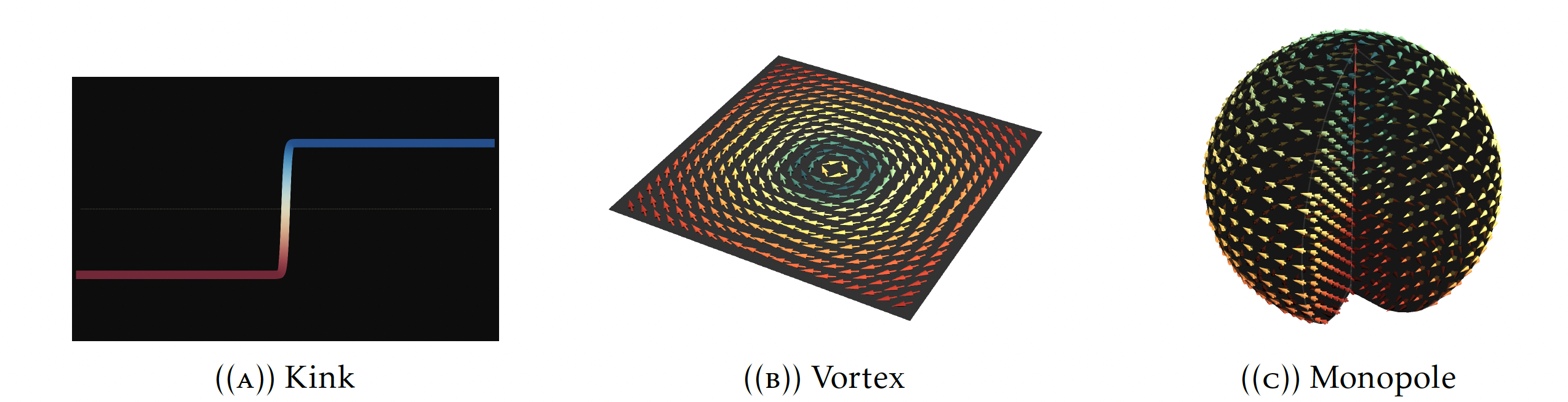
An incredibly subtle but important concept in modern Physics is that of topological terms. A theory purely containing these terms is known as a topological field theory. When the fields in such theories are or can be recast in terms of gauge fields, we talk about topological gauge theories. We use this terminology more loosely to describe those theories, in general coupled to matter, in which topological gauge terms are present. In a nutshell, these describe systems in which the gauge field presents topological features. Roughly speaking, these features come in the form of twists, singularities, discontinuities, branch-cuts, or other ill-defined countable mathematical objects, that are found in the target space of a gauge potential or its field strength. These defects seed topological invariants that label robust sectors or regimes in which the systems can be found. There is a deep connection between quantum anomalies, topological terms, fractional fermion numbers, index theorems, and geometric phases that is often difficult to make explicit.
Quantum Matter
Quantum Mechanics describes the wonders of Nature in the “micro-world”. The fascinating phenomenology at the atomic scale does not, however, survive its transition to larger, more mundane dimensions. This does not necessarily mean that Quantum Mechanics is only valid for tiny things, but rather, that its magic is blurred by the complexity and messiness of everyday reality, which we call the Classical world. Macroscopic quantum phenomena are an exception to this rule, implying that something extraordinary is preventing the fading of this “quantumness”. Their study constitutes a major field of research as they might help us take some of the Quantum richness to our prosaic Classical realm. Some of these effects can be understood under a guiding and unifying principle, i.e. Symmetry. Some others, more recently discovered, require new tools and their origin seems to be traced back to a different concept, i.e. Topology. Nowadays, there is an intertwining between both types of systems, so their distinction and interplay is rapidly becoming fuzzy, maybe in favour of a — yet to emerge — deeper organising principle that brings them all together.
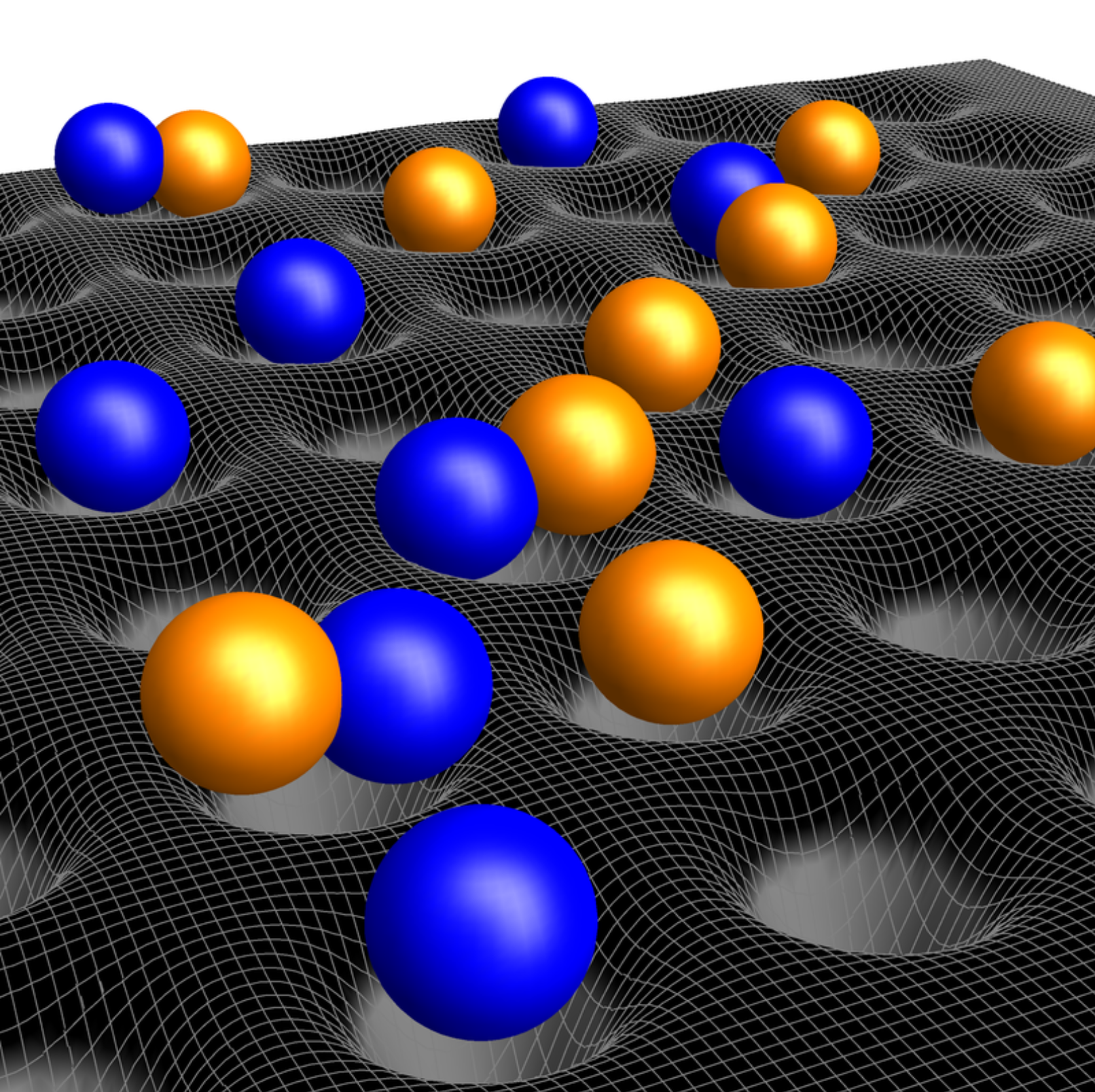
Quantum Fluids
Quantum fluids are states of matter with the ability to flow (e.g. gases and liquids) whose description and properties are manifestly quantum-mechanical. Most of the modern theory of Quantum Many-Body Physics is based on the study of these systems. Prominent groups of them are condensates and superfluids.
Fractionalisation & Topological Order
To be continued…
Synthetic Gravity
A microscopic understanding of gravity remains one of the major unsolved mysteries of the Universe. It was realised early on that there is an intrinsic tension between Quantum Mechanics and General Relativity when both quantum-mechanical and gravitational effects are sufficiently strong and coexist. Resolving this conflict seems to require a quantisation of gravity, an accommodation of classical gravity to quantum setting, or a new reformulation of fundamental Physics.
The former approach has historically been, by far, the most popular. Gravity is famously hard to quantise due to its non-renormalisability. This has lead to a colossal body of work and eminent figures developing theories of quantum gravity. Some of these programs, like string theory, provide not only a way to quantum gravity but to a theory of everything. However, it is not clear that gravity must be quantised in the first place. Should it not be, one would need to consistently explain the incoherences in the coexistence of quantum-mechanical systems in the presence of classical gravity.
In this conundrum, it does not appear unreasonable to revisit the basics and get familiar with the inconsistencies and paradoxes appearing in this scenario, now that quantum-mechanical systems can be controlled to an unprecedented level. Table-top experiments might offer intuition and unambiguous ways to clarify some of these issues. There are, at least, two major ways in which table-top experiments are relevant to this problem: (i) Those in which microscopic tests of gravity are expected to shed light onto either its “classicality” or ”quantumness”, which settles the debate and propels research on a clearer path; and (ii) those which are engineered or synthetic analogues of gravitational systems are realised on quantum setups. The purpose of the latter is meant as experimental “proofs of concept” of theoretical ideas. We might refer to the latter as synthetic gravity.

Dualities
A duality is the ability of an entity to be “expressed” or “observed” in two complementary ways, like two different shadows of the same object. This abstract object can be a physical phenomenon, but it can also be a mathematical description. Some mathematical theories (or models) can be dual to each other, meaning that there is an exact mathematical identity connecting them, even though they are apparently very different. Well-known examples of duality are electro-magnetism, particle-wave behaviour of quantum entities, the Krammers-Wannier duality in spin systems, T and S dualities in string theory, the Anti-de-Sitter/Conformal-Field-Theory correspondence, or the Langlands program. In fact, dualities are pretty common in Physics. Yet, they are some of the more unsettling and misunderstood concepts in the field.
The Composite Particle Duality
The composite particle duality extends the notions of both flux attachment and statistical transmutation in spacetime dimensions beyond (2+1)D. It constitutes an exact correspondence that can be understood both as a framework and as a physical mechanism. The immediate implication of the duality is that an interacting quantum system in arbitrary dimensions can experience a modification of its statistical properties if coupled to a certain gauge field. In other words, commutation relations of quantum fields can be effectively modified by a dynamical physical process. For instance, an originally bosonic quantum fluid in d spatial dimensions can feature composite fermionic (or anyonic) excitations when coupled to a statistical gauge field . This opens the door to a new realm of topological phases both in lattice and continuum and across dimensions.
Other Interests
- Strongly-Correlated Systems
- Anomalies in Field Theory and their Physical Manifestations
- Topological Solitons & Instantons
- Quantum Hydrodynamics & Shock Waves
- Frustrated Magnetism
- Knot Theory
- Integrable Models
- String Theory
- Geometric Group Theory